Tutorial: Creating a Multiple Choice Scanner with OpenCV
Source code : https://github.com/ayoungprogrammer/MultipleChoiceScanner
Algorithm
1. Image Preprocesssing
cv::Size size(3,3); cv::GaussianBlur(img,img,size,0); adaptiveThreshold(img, img,255,CV_ADAPTIVE_THRESH_MEAN_C, CV_THRESH_BINARY,75,10); cv::bitwise_not(img, img);
2. Hough transfrom to get lines
cv::Mat img2;
cvtColor(img,img2, CV_GRAY2RGB);
vector<Vec4i> lines;
HoughLinesP(img, lines, 1, CV_PI/180, 80, 400, 10);
for( size_t i = 0; i < lines.size(); i++ )
{
Vec4i l = lines[i];
line( img2, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0,0,255), 3, CV_AA);
}
3. Find POI of lines
However, we need to sort the points from top left to bottom right:
bool comparator(Point2f a,Point2f b){
return a.x<b.x;
}
void sortCorners(std::vector<cv::Point2f>& corners, cv::Point2f center)
{
std::vector<cv::Point2f> top, bot;
for (int i = 0; i < corners.size(); i++)
{
if (corners[i].y < center.y)
top.push_back(corners[i]);
else
bot.push_back(corners[i]);
}
sort(top.begin(),top.end(),comparator);
sort(bot.begin(),bot.end(),comparator);
cv::Point2f tl = top[0].x;
cv::Point2f tr = top[top.size()-1];
cv::Point2f bl = bot[0];
cv::Point2f br = bot[bot.size()-1];
corners.clear();
corners.push_back(tl);
corners.push_back(tr);
corners.push_back(br);
corners.push_back(bl);
}
// Get mass center
cv::Point2f center(0,0);
for (int i = 0; i < corners.size(); i++)
center += corners[i];
center *= (1. / corners.size());
sortCorners(corners, center);
4. Apply a perspective transform
// Get transformation matrix cv::Mat transmtx = cv::getPerspectiveTransform(corners, quad_pts); // Apply perspective transformation cv::warpPerspective(img3, quad, transmtx, quad.size());
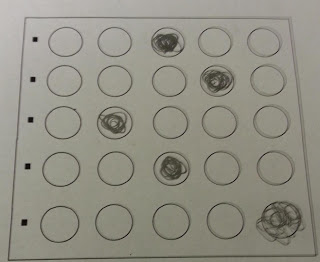
5. Find circles
cvtColor(img,cimg, CV_BGR2GRAY);
vector<Vec3f> circles;
HoughCircles(cimg, circles, CV_HOUGH_GRADIENT, 1, img.rows/16, 100, 75, 0, 0 );
for( size_t i = 0; i < circles.size(); i++ )
{
Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
int radius = cvRound(circles[i][2]);
// circle center
circle( testImg, center, 3, Scalar(0,255,0), -1, 8, 0 );
// circle outline
6. Sort circles into rows and columns
y1 = y coordinate of centre of circle 1
y2 = y coordinate of centre of circle 2
r = radius
y2-r > y1 and y2+r<y1
If two circles pass this test, then we can say that they are in the same row. We do this to all the circle until we have figure out which circles are in which rows.Row is an array of data about each row and index. The double part of the pair is the y coord of the row and the int is the index of arrays in bubble (used for sorting).
vector<vector<Vec3f> > bubble;
vector<pair<double,int> > row;
for(int i=0;i<circles.size();i++){
bool found = false;
int r = cvRound(circles[i][2]);
int x = cvRound(circles[i][0]);
int y= cvRound(circles[i][1]);
for(int j=0;j<row.size();j++){
int y2 = row[j].first;
if(y-r<y2&&y+r>y2){
bubble[j].push_back(circles[i]);
found = true;
break;
}
}
if(!found){
int l = row.size();
row.push_back(make_pair(y,l));
vector<Vec3f> v;
v.push_back(circles[i]);
bubble.push_back(v);
}
found = false;
}
Then sort the rows by y coord and inside each row sort by x coord so you will have a order from top to bottom and left to right.
bool comparator2(pair<double,int> a,pair<double,int> b){
return a.first<b.first;
}
bool comparator3(Vec3f a,Vec3f b){
return a[0]<b[0];
}
....
sort(row.begin(),row.end(),comparator2);
for(int i=0;i<bubble.size();i++){
sort(bubble[i].begin(),bubble[i].end(),comparator3);
}
7. Check bubble
for(int i=0;i<row.size();i++){
double max = 0;
int ind = -1;
for(int j=0;j<bubble[row[i].second].size();j++){
Vec3f cir = bubble[row[i].second][j];
int r = cvRound(cir[2]);
int x = cvRound(cir[0]);
int y= cvRound(cir[1]);
Point c(x,y);
// circle outline
circle( img, c, r, Scalar(0,0,255), 3, 8, 0 );
Rect rect(x-r,y-r,2*r,2*r);
Mat submat = cimg(rect);
double p =(double)countNonZero(submat)/(submat.size().width*submat.size().height);
if(p>=0.3 && p>max){
max = p;
ind = j;
}
}
if(ind==-1)printf("%d:-",i+1);
else printf("%d:%c",i+1,'A'+ind);
cout<<endl;
}
}
Source code here: https://github.com/ayoungprogrammer/MultipleChoiceScanner





Leave a Reply