Tag: extraction

So once again, we’ll use my favourite snippet for cleaning up an image:

Apply a Gaussian blur and using an adaptive threshold for binarzing the image

//Apply blur to smooth edges and use adapative thresholding  
 cv::Size size(3,3);  
 cv::GaussianBlur(img,img,size,0);  
 adaptiveThreshold(img, img,255,CV_ADAPTIVE_THRESH_MEAN_C, CV_THRESH_BINARY,75,10);  
 cv::bitwise_not(img, img);  

Use a probabilistic Hough line detection to figure out where the lines are. This algorithm works by going through every point in the image and checking every angle. 

 vector<Vec4i> lines;  
 HoughLinesP(img, lines, 1, CV_PI/180, 80, 100, 10);  

And here we have the results of the algorithm:

This is the most complex part of the algorithm (general pseudocode):

First, initialize every line to be in an undefined group

For every line compute the intersection of the two line segments (if they do not intersect ignore the point)

      If both lines are undefined, make a new group out of them

      If only one line is defined in a group, add the other line into the group. 

      If both lines are defined than add all the lines from one group into the other group

      If both lines are in the same group, do nothing

Intersection function: (modified from: http://opencv-code.com/tutorials/automatic-perspective-correction-for-quadrilateral-objects/)

cv::Point2f computeIntersect(cv::Vec4i a, cv::Vec4i b)  
 {  
   int x1 = a[0], y1 = a[1], x2 = a[2], y2 = a[3];  
   int x3 = b[0], y3 = b[1], x4 = b[2], y4 = b[3];  
   if (float d = ((float)(x1-x2) * (y3-y4)) - ((y1-y2) * (x3-x4)))  
   {  
     cv::Point2f pt;  
     pt.x = ((x1*y2 - y1*x2) * (x3-x4) - (x1-x2) * (x3*y4 - y3*x4)) / d;  
     pt.y = ((x1*y2 - y1*x2) * (y3-y4) - (y1-y2) * (x3*y4 - y3*x4)) / d;  
           //-10 is a threshold, the POI can be off by at most 10 pixels
           if(pt.x<min(x1,x2)-10||pt.x>max(x1,x2)+10||pt.y<min(y1,y2)-10||pt.y>max(y1,y2)+10){  
                return Point2f(-1,-1);  
           }  
           if(pt.x<min(x3,x4)-10||pt.x>max(x3,x4)+10||pt.y<min(y3,y4)-10||pt.y>max(y3,y4)+10){  
                return Point2f(-1,-1);  
           }  
     return pt;  
   }  
   else  
     return cv::Point2f(-1, -1);  
 }  

Connected components

int* poly = new int[lines.size()];  
  for(int i=0;i<lines.size();i++)poly[i] = - 1;  
  int curPoly = 0;  
       vector<vector<cv::Point2f> > corners;  
      for (int i = 0; i < lines.size(); i++)  
      {  
           for (int j = i+1; j < lines.size(); j++)  
           {  
          
                cv::Point2f pt = computeIntersect(lines[i], lines[j]);  
                if (pt.x >= 0 && pt.y >= 0&&pt.x<img2.size().width&&pt.y<img2.size().height){  
              
                     if(poly[i]==-1&&poly[j] == -1){  
                          vector<Point2f> v;  
                          v.push_back(pt);  
                          corners.push_back(v);       
                          poly[i] = curPoly;  
                          poly[j] = curPoly;  
                          curPoly++;  
                          continue;  
                     }  
                     if(poly[i]==-1&&poly[j]>=0){  
                          corners[poly[j]].push_back(pt);  
                          poly[i] = poly[j];  
                          continue;  
                     }  
                     if(poly[i]>=0&&poly[j]==-1){  
                          corners[poly[i]].push_back(pt);  
                          poly[j] = poly[i];  
                          continue;  
                     }  
                     if(poly[i]>=0&&poly[j]>=0){  
                          if(poly[i]==poly[j]){  
                               corners[poly[i]].push_back(pt);  
                               continue;  
                          }  
                        
                          for(int k=0;k<corners[poly[j]].size();k++){  
                               corners[poly[i]].push_back(corners[poly[j]][k]);  
                          }  
                       
                          corners[poly[j]].clear();  
                          poly[j] = poly[i];  
                          continue;  
                     }  
                }  
           }  
      }  

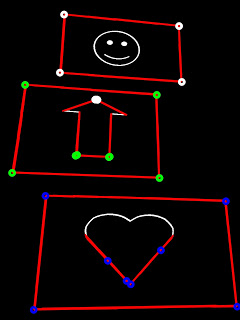
The circles represent the points of intersection and the colours represent the different shapes. 

Now we need to find corners of the polygons to get the polygon formed from the point of intersections.

Pseudocode:

For each group of points:

       Compute mass center (average of points)

        For each point that is above the mass center, add to top list

        For each point that is below the mass center, add to bottom list

        Sort top list and bottom list by x val

       first element of top list is  left most (top left point)

        last element of top list is right most (top right point) 

       first element of bottom list is  left most  (bottom left point)

       

 bool comparator(Point2f a,Point2f b){  
           return a.x<b.x;  
      }  
 void sortCorners(std::vector<cv::Point2f>& corners, cv::Point2f center)  
 {  
   std::vector<cv::Point2f> top, bot;  
   for (int i = 0; i < corners.size(); i++)  
   {  
     if (corners[i].y < center.y)  
       top.push_back(corners[i]);  
     else  
       bot.push_back(corners[i]);  
   }  
      sort(top.begin(),top.end(),comparator);  
      sort(bot.begin(),bot.end(),comparator);  
   cv::Point2f tl = top[0];
   cv::Point2f tr = top[top.size()-1];
   cv::Point2f bl = bot[0];
   cv::Point2f br = bot[bot.size()-1];  
   corners.clear();  
   corners.push_back(tl);  
   corners.push_back(tr);  
   corners.push_back(br);  
   corners.push_back(bl);  
 }  

for(int i=0;i<corners.size();i++){  
           cv::Point2f center(0,0);  
           if(corners[i].size()<4)continue;  
           for(int j=0;j<corners[i].size();j++){  
                center += corners[i][j];  
           }  
           center *= (1. / corners[i].size());  
           sortCorners(corners[i], center);  
      }  

The final step is extract each rectangle from the image. We can do this quite easily with the perspective transform from OpenCV. To get an estimate of the dimensions of the rectangle we can use a bounding rectangle of the corners. If the dimensions of that rectangle are under our wanted area, we ignore the polygon. If the polygon also has less than 4 points we can ignore it as well. 

for(int i=0;i<corners.size();i++){  
           if(corners[i].size()<4)continue;  
           Rect r = boundingRect(corners[i]);  
           if(r.area()<50000)continue;  
           cout<<r.area()<<endl;  
           // Define the destination image  
           cv::Mat quad = cv::Mat::zeros(r.height, r.width, CV_8UC3);  
           // Corners of the destination image  
           std::vector<cv::Point2f> quad_pts;  
           quad_pts.push_back(cv::Point2f(0, 0));  
           quad_pts.push_back(cv::Point2f(quad.cols, 0));  
           quad_pts.push_back(cv::Point2f(quad.cols, quad.rows));  
           quad_pts.push_back(cv::Point2f(0, quad.rows));  
           // Get transformation matrix  
           cv::Mat transmtx = cv::getPerspectiveTransform(corners[i], quad_pts);  
           // Apply perspective transformation  
           cv::warpPerspective(img3, quad, transmtx, quad.size());  
           stringstream ss;  
           ss<<i<<".jpg";  
           imshow(ss.str(), quad);  
      }