Introduction

Encoding numerical inputs for neural networks is difficult because the representation space is very large and there is no easy way to embed numbers into a smaller space without losing information. Some of the ways to currently handle this is:

• Scale inputs from minimum and maximum values to [-1, 1]
• One hot for each number
• One hot for different bins (e.g. [0-0], [1-2], [3-7], [8 – 19], [20, infty])

In small integer number ranges, these methods can work well, but they don’t scale well for wider ranges. In the input scaling approach, precision is lost making it difficult to distinguish between two numbers close in value. For the binning methods, information about the mathematical properties of the numbers such as adjacency and scaling is lost.

The desideratum of our embeddings of numbers to vectors are as follows:

• able to handle numbers of arbitrary length
• captures mathematical relationships between numbers (addition, multiplication, etc.)
• able to model sequences of numbers

In this blog post, we will explore a novel approach for embedding numbers as vectors that include these desideratum.

Approach

My approach for this problem is inspired by word2vec but unlike words which follow the distributional hypothesis, numbers follow the the rules of arithmetic. Instead of finding a “corpus” of numbers to train on, we can generate random arithmetic sequences and have our network “learn” the rules of arithmetic from the generated sequences and as a side effect, be able to encode numbers as vectors and  sequences as vectors.

Problem Statement

Given a sequence of length n integers \(x_1, x_2 \ldots x_n\), predict the next number in the sequence \(x_{n+1}\).

Architecture

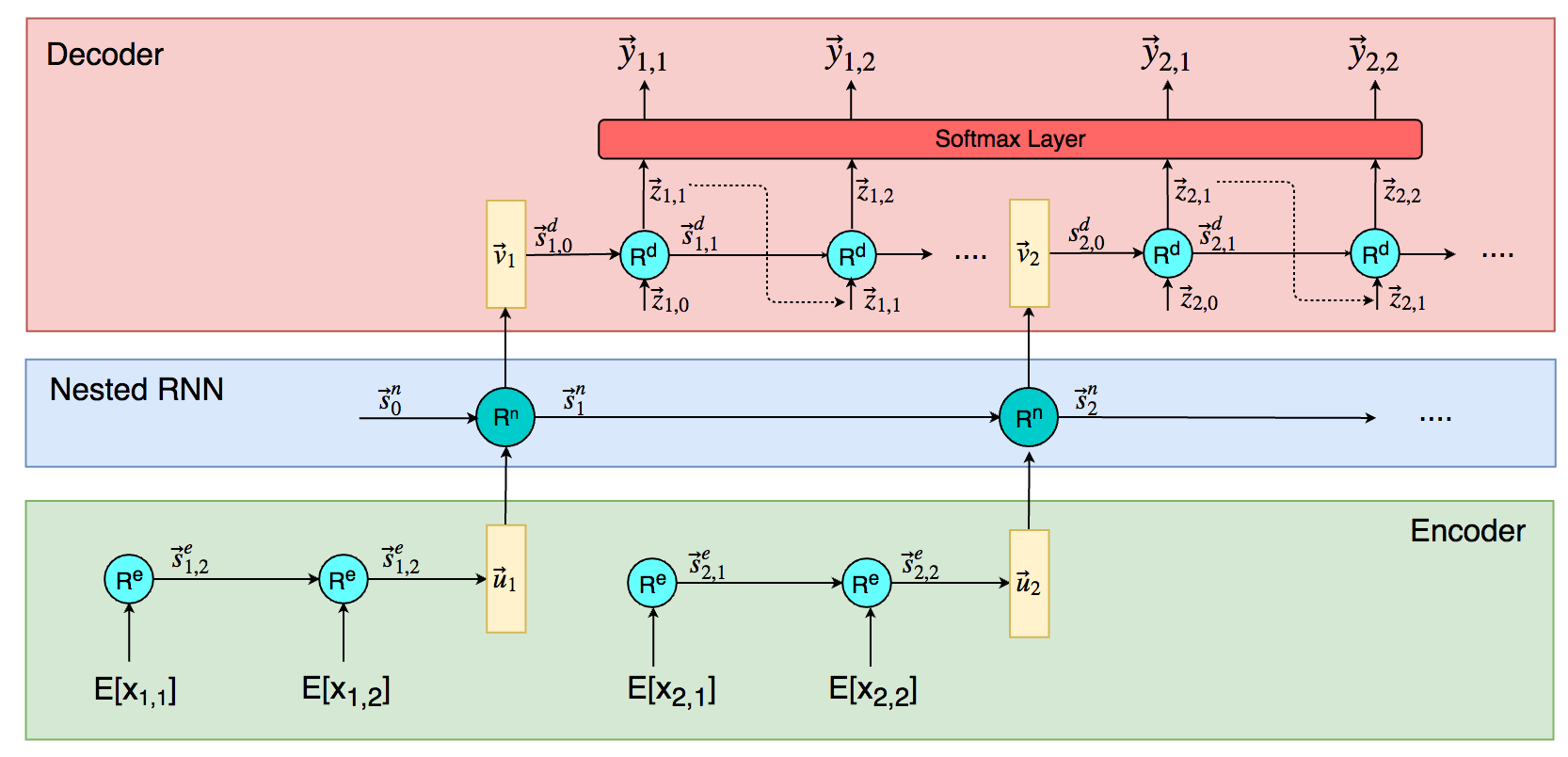
The architecture of the system consists of three parts: the encoder, the decoder and the nested RNN.

The encoder is an RNN that takes a number represented as a sequence of digits and encodes it into a vector that represents an embedded number.

The nested RNN takes the embedded numbers and previous state to output another embedded vector that represents the next number.

The decoder then takes the embedded number and unravels it through the decoder RNN to output the digits of the next predicted number.

Formally:

Let \(X\) represent a sequence of natural numbers where \(X_{i,j}\) represents the j-th digit of the i-th number of the sequence. We also append an <eos> “digit” to the end of each number to signal the end of the number. For the sequence X = 123, 456, 789, we have \(X_{1,2} = 2, X_{3,3} = 9, X_{3,4} = <eos>\).

Let \(l_i\) be the number of digits in the i-th number of the sequence (including <eos> digit. Let \(E\) be an embedding matrix for each digit.

Let \(\vec{u}_i\) be an embedding of the i-th number in a sequence. It is computed as the final state of the encoder. Let \(\vec{v}_i\) be an embedding of the predicted (i+1)-th number in a sequence. It is computed from the output of the nested RNN and used as the initial state of the decoder.

Let \(R^e, R^d, R^n\) be the functions that gives the next state for the encoder, decoder and nested RNN respectively. Let \(O^d, O^n\) be the functions that gives the output of the current state for the decoder and nested RNN respectively.

Let \(\vec{s}^e_{i,j}\) be the state vector for \(R^e\) for the j-th timestep of the i-th number of the sequence. Let \(\vec{s}^d_{i,j}\) be the state vector for \(R^d\) for the j-th timestep of the i-th number of the sequence. Let \(\vec{s}^n_i\) represent the state vector of \(R^n\) for the i-th timestep.

Let \(z_{i,j}\) be the output of \(R^d\) at the j-th timestep of the i-th number of the sequence.

Let \(\hat{y}_{i,j}\) represent the distribution of digits for the prediction of the j-th digit of the (i+1)th number of the sequence.

\(\displaystyle{\begin{eqnarray}\vec{s}^e_{i,j} &=& R^e(E[X_{i,j}], \vec{s}^e_{i, j-1})\\\vec{u}_i &=& \vec{s}^e_{i,l_i}\\ \vec{s}^n_i &=& R^n(\vec{u}_i, \vec{s}^n_{i-1})\\\vec{v_i} &=& O^n(\vec{s}^n_i)\\ \vec{z}_{i,j} &=& O^d(\vec{s}^d_{i,j})\\ \vec{s}^d_{i, j} &=& R^d(\vec{z}_{i,j-1}, \vec{s}^d_{i, j-1})\\ \hat{y}_{i,j} &=& \text{softmax}(\text{MLP}(\vec{z}_{i,j}))\\ p(X_{i+1,j})=k |X_1, \ldots, X_i, X_{i+1, 1}, \ldots X_{i+1, j-1}) &=& \hat{y}_{i,j}[k]\end{eqnarray}}\)

We use a cross-entropy loss function where \(y_{i,j}[t]\) represents the correct digit class for \(y_{i,j}\):

\(\displaystyle{\begin{eqnarray}L(y, \hat{y}) &=& \sum_i \sum_j -\log \hat{y}_{i,j}[t]\end{eqnarray} }\)

Since I also find it difficult to intuitively understand what these sets of equations mean, here is a clearer diagram of the nested network:

Training

The whole network is trained end-to-end by generating random mathematical sequences and predicting the next number in the sequence. The sequences generated contains addition, subtraction, multiplication, division and exponents. The sequences generated also includes repeating series of numbers.

After 10,000 epochs of 500 sequences each, the networks converges and is reasonably able to predict the next number in a sequence. On my Macbook Pro with a Nvidia GT750M, the network implemented on Tensorflow took 1h to train.

Results

Taking a look at some sample sequences, we can see that the network is reasonably able to predict the next number.

Seq [43424, 43425, 43426, 43427]
Predicted [43423, 43426, 43427, 43428]
Seq [3, 4, 3, 4, 3, 4, 3, 4, 3, 4]
Predicted [9, 5, 4, 3, 4, 3, 4, 3, 4, 3]
Seq [2, 4, 8, 16, 32, 64, 128]
Predicted [4, 8, 16, 32, 64, 128, 256]
Seq [10, 9, 8, 7, 6, 5, 4, 3]
Predicted [20, 10, 10, 60, 4, 4, 3, 2]

With the trained model, we can compute embeddings of individual numbers and visualize the embeddings with the t-sne algorithm.

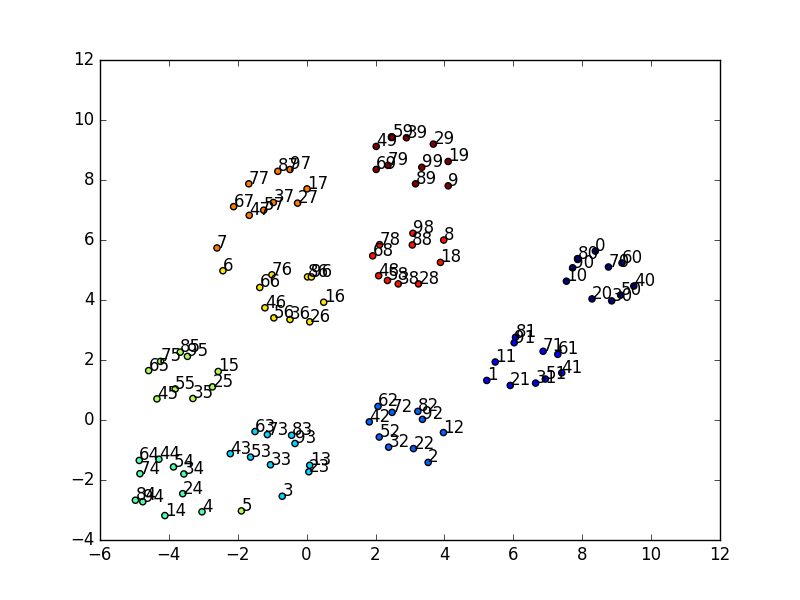
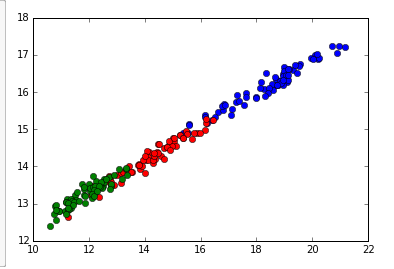
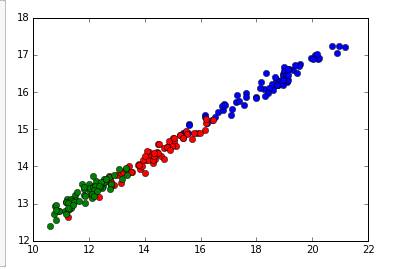
We can see an interesting pattern when we plot the first 100 numbers (color coded by last digit). Another interesting pattern to observe is within clusters, the numbers also rotate clockwise or counterclockwise.

We can also trace the path of the embeddings sequentially, we can see that there is some structure to the positioning of the numbers.

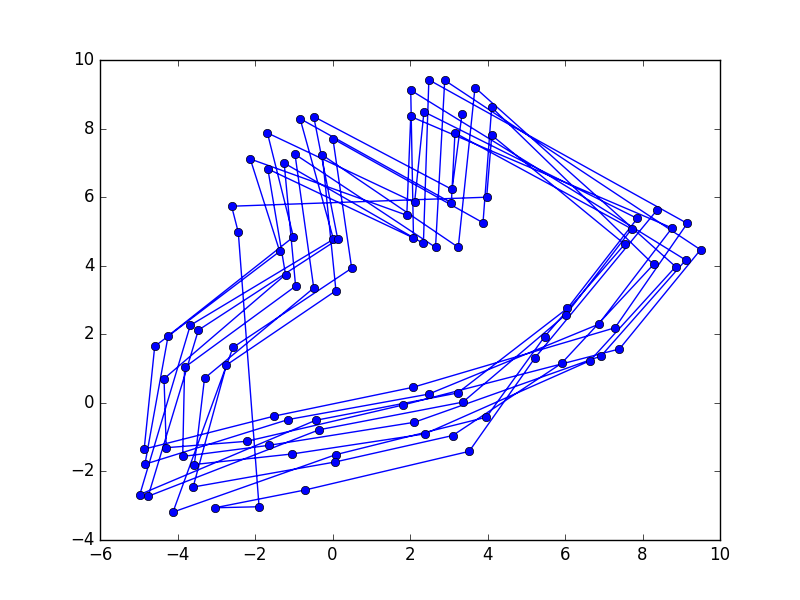
If we look at the visualizations of the embeddings for numbers 1-1000 we can see that the clusters still exist for the last digit (each color corresponds to numbers with the same last digit)

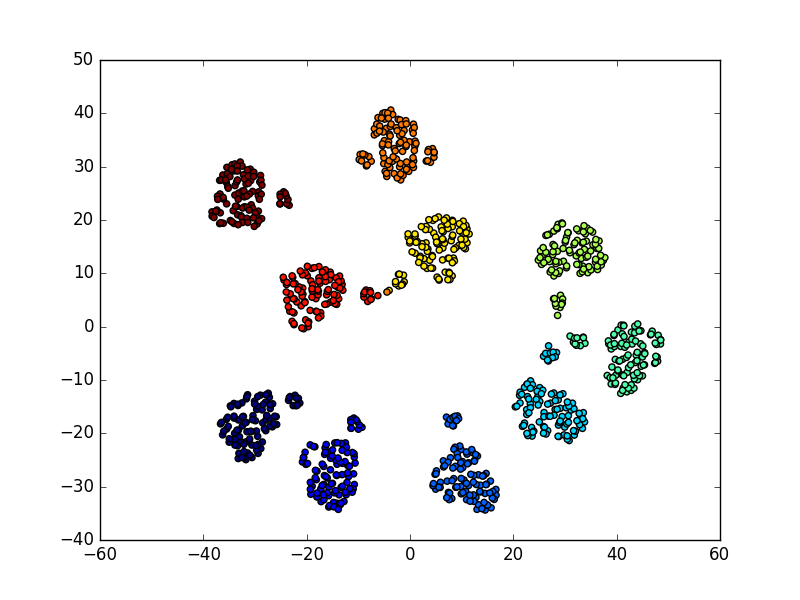
We can also see the same structural lines for the sequential path for numbers 1 to 1000:

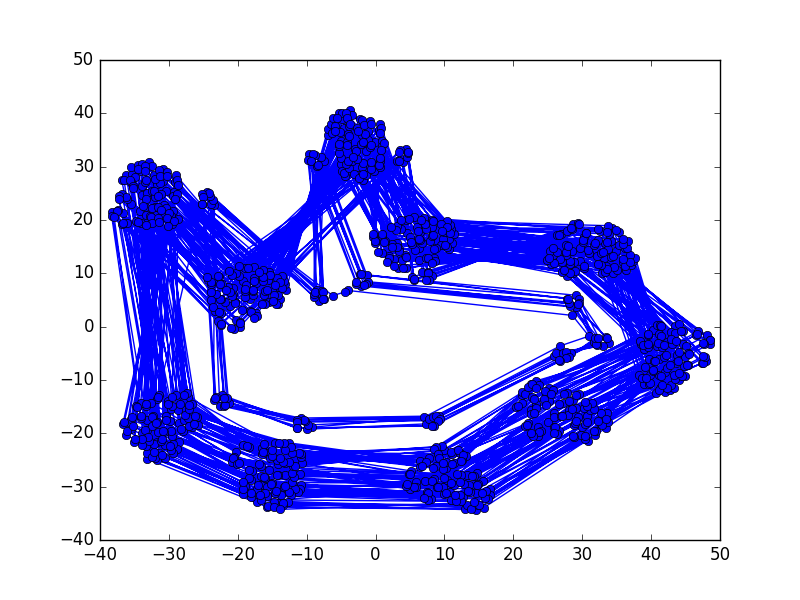
The inner linear pattern is formed from the number 1-99 and the outer linear pattern is formed from the numbers 100-1000.

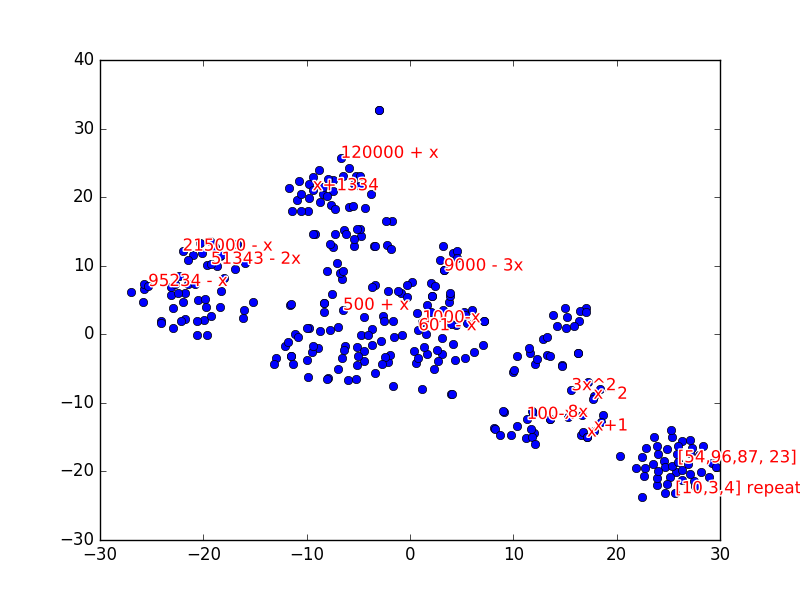
We can also look at the embeddings of each sequence by taking the vector \(\vec{s}^n_k\) after feeding in k=8 numbers of a sequence into the model. We can visualize the sequence embeddings with t-sne using 300 sequences:

From the visualization, we can see that similar sequences are clustered together. For example, repeating patterns, quadratic sequences, linear sequences and large number sequences are grouped together. We can see that the network is able to extract some high level structure for different types of sequences.

Using this, we can see that if we encounter a sequence we can’t determine a pattern for, we can find the nearest sequence embedding to approximate the pattern type.

Code: Github

The model is written in Python using Tensorflow 1.1. The code is not very well written due to the fact that I was forced to use an outdated version of TF with underdeveloped RNN support because of OS X GPU compatibility reasons.

The code is a proof of a concept and comes from the result of stitching together outdated tutorials together.

Further improvements:

• bilateral RNN
• stack more layers
• attention mechanism
• beam search
• negative numbers
• teacher forcing